Where the techniques of Maths
are explained in simple terms.
Probability - Probability trees.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| The questions on this page focus on: |
| 1. basic probability. |
| 2. constant probability. |
| 3. probability with replacement. |
| 4. probability without replacement. |
| 5. harder contexts. |
| 6. incomplete trees. |
| Basic | 1. There are 12 students in a room. Four of them speak Arabic only, three speak Spanish only and the rest speak English only.
If two students are selected at random, find the probability that: Answer.(i) Pr(EE) = 5/33 (ii) Pr(neither E) = 7/22. (iii) Pr (not same language) = 47/66. |
| 2. A six-sided die is rolled 10 times.
What is the probability that the number 6 does not appear in the 10 rolls? Answer.Pr(no 6) = 0.162 (3 dp). |
|
| 3. In a class I know well, there are 30 students. 40% are boys and 60% are girls (girls love maths more!!). I select two students at random (we all get on well) to help me hang some great maths posters I just purchased.
What is the probability that: Answer.(i) (a) Pr(GG) = 0.36 (ii) Pr(GB) = 0.48. (iii) Pr (BB) = 0.16. |
|
4. In one container I have 3 red balls and 4 black balls. In a second container I have 2 red and 7 black balls. I draw one ball from each container. What is the probability of selecting:
Answer.(i) Pr(RR) = 2/21. (ii) Pr(≥ 1R) = 5/9. (iii) Pr (≤ 1) = 19/21. |
|
| 5. The probability that the temperature will fall below -10° on any day through winter at a particular city in the northern hemisphere is 0.85.
What is the probability that the temperature in this city will fall below -10° on at least one day of the weekend? Answer.Pr(at least one day) =1 - Pr(not on 2 days) = 0.98 |
|
| 6. The probability that Harley will pass a Maths test is 0.6, a PDHPE test is 0.8 and a Geography test is 0.7.
When he sits for these three tests at his Trial, what is the probability that Harley: Answer.(i) Pr (passes one) = 0.336 (ii) Pr (passes all 3) = 0.188 (iii) Pr (at least 1) = 0.976. |
|
7. I have a friend who forgot her 4 digit PIN number for the ATM. The PIN is of course made from the integers 0 to 9.
Answer.(i) Pr(correct) = 1/10,000 (ii) 1 - (1/10)4 = 3,439/10,000 (iii) 1/1,000 (iv) 1/24 |
|
8. Two BMX cross-country riders compete in a difficult event. Organisers anticipate that Jeff has a 60% chance of finishing the event while they give Ben a 40% chance of finishing. What is the probability that: Answer.(i) Pr(both finish) = 0.24 (ii) Prob (only 1 finishes) = 0.52. |
|
| 9. | |
| Constant probability. | 10. A biassed coin is such that the probability of getting a head is 5/8. The coin is tossed twice.
Answer.(i) (a) Pr(HH) = 25/64 (ii) Pr(TT) = 9/64. (iii) Pr (HT) = 15/32. (iv) Pr( T) = 3/8. |
| 11. The chance of rain on any day during July is given as being 1 in 10. What is the chance (to 3 decimal places)of: Answer.(i) (a) Pr(RRR) = 0.001 (ii) Pr(RR RR RR) = 0.000 - there is a chance but highly unlikely. (iii) Pr (RFRFR) = 0.001. (iv) Pr(FFFFF) = 0.590. |
|
| 12. Phoebe is starting a new job and will be catching the B-line bus from Mona Vale to the City. Her new employer tells her that if she is late on both of the first two days, she will be terminated.
The probability of the bus being on time is 0.97. Answer.(i) (a) Pr (late day 1) = 0.03 (ii) Pr (late both days) = 0.0009. (iii) Pr (keeping job) = 0.9991. (iv) Pr (late once) = 0.085 (3 dp). |
|
| 13. Roses are prone to attack by aphids so a new form of spray has been developed which does not affect the ladybirds (who eat a lot of aphids). Tests have shown that the spray is 80% successful in eliminating the aphids.
Two rose plants are selected at random and sprayed. What is the probability that: Answer.(i) (a) Pr (elim in both) = 16/25 (ii) Pr (elim in one) = 8/25. (iii) Pr (at least 1) = 9/25. |
|
| 14. The probability of James hitting a moving target with an arrow is 0.2.
What is the least number of arrows James must shoot at a moving target if his probability to hit it at least once is to exceed 80%? Answer.8 times is the minimum. |
|
| With replacement | 15. From an urn containing 4 red and 7 white balls, two balls are drawn in succession with replacement. Find:
Answer.(i) Pr(W) = 7/11 (ii) Pr(?W) = 7/11. (iii) Pr (WW) = 21/55. (iv) Pr(at least 1 W) = 49/55. |
16. A card is selected from a normal deck of 42 cards containing 13 cards of each of the suits clubs, spades (both black cards), hearts and diamonds (both are red cards). The suit is noted and then the card is returned to the deck. A second card is then chosen at random.
Answer.(ii) Pr(HH) = 1/16. (iii) Pr(RR) = 1/4. (iv) Pr (CD or DC) = 1/4. (v) Pr(at least 1 H) = 1 - 9/16 = 7/16. |
|
| 17. | |
| 18. | |
| 10. | |
| Without replacement | 11.From an urn containing 4 red and 7 white balls, two balls are drawn in succession without replacement. Find:
Answer.(i) Pr(W) = 7/11. (ii) Pr(?W) = 7/11. (iii) Pr (WW) = 49/121. (iv) Pr( at least 1 W) = 105/121. |
12. Grace buys 4 tickets in a raffle. There is a total of 100 tickets being sold. The prizes on offer are $40 for first prixe,, $30 for second prize and $20 for third prize. Find the probability that Grace:
Answer.(i) Pr(wins $70) = 1/40425 (ii) Pr(wins $30) = 16/13475. (iii) Pr (wins a prize) = 941/8085. (iv) Pr( at least 1 W) = 49/55. |
|
| 13. There are six balls in an urn. They are numbered with the digits 1 to 6. The balls are drawn one at a time.
What is the probability that: Answer.(i) Pr(3 is 1st ball) = 1/6 (ii) Pr(2 or 4) = 1/3. (iii) Pr (product = 12) = 2/15. |
|
| 14. Two containers contain red and green counters. Container 1 has 6 green and 3 red counters while Container 2 has 4 green and 7 red counters.
Yoko selects one of the containers and removes two counters without replacement. Answer.(i) Pr (2 green from # 2) = 3/55 (ii) Pr (≥ 1 green from # 2) = 17/55. |
|
| 15. Sam has 2 pairs of grey socks and 3 pairs of black socks.
On Mondays, Wednesdays and Fridays, he selects one pair of socks at random to wear. Naturally, Sam only wears a pair of socks once!! Answer.(i) Pr (black) = 3/5 (ii) Pr (same colour) = 1/10. (iii) Pr (GBG or BGB) = 3/10. |
|
| 16. Alyssa is given a box of chocolates as a reward for passing her driving test. There are 10 chocolates in the box and, although they all look identical, three chocolates have caramel centres and the rest have mint centres.
Alyssa - showing great restraint - only selects three chocolates at random. Find the probability that: (i) Alyssa east three mint chocolates. (ii) Alyssa eats exactly one caramel chocolate. Answer.(i) 7/24.(ii) 21/40. |
|
17. There are four eggs remaining in a carton. It is known that one of the eggs is cracked. Two eggs are selected at random.
|
|
| 18. A box contains five black marbles and five white marbles. Monica selects three marbles from the box without replacing them.
What is the probability that at least one of the selected marbles is white? Answer.(i) 11/12. |
|
| Harder | Bag A contains 4 blue balls and 3 red balls. Bag B contains 2 blue balls and 3 red balls.
A person selects one of the 7 balls from Bag A and puts it into Bag B. She then selects a ball from Bag B. What is the chance that the ball selected from Bag B is red? Answer.Pr (red from Bag B) = 4/7. |
| Mutually exclusive events. | 21. In a game of football, the probability that Damien will tackle an opposing player is 0.7. If Damien does not tackle that player, the probability than Nathan makes the tackle on the attacking player is 0.4.
Find the probability that an attacking player is tackled. Answer.Pr(tackle) = 0.82 |
| 22. The probability that Georgia meets her perfect partner is 5%.
She keeps meeting people but intends to stop when she meets her ideal person. Answer.(i) (a) Pr (3rd) = (0.95)2×0.05 (ii) Pr (3 or less) = 0.05 + 0.95×0.05 + 0.952×0.05. (iii) Pr (no more than 10) = 0.401. (iv) number to meet is 59 - a great social life ahead!!. |
|
| 23. The local model boat club has eight equally boats. Three are green, four are blue and one is red.
If two races are held, what is the probability that: Answer.(i) (a) Pr (BB) = 0.25 (ii) Pr (not G) = 25/64. (iii) Pr (diff cols) = 19/32. (iv) Pr(BB or GG) = 9/28. |
|
24. Charlotte and Ben play a game of dice where they take turns in throwing two unbiassed dice. The winner is the first person to throw a double. Ben throws first (he is younger than Charlotte).
Answer.(i) (a) Pr (Charlotte wins) = 6/11. |
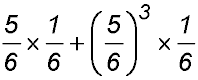 .
.